Analysis of Network Clustering Algorithms and Cluster Quality Metrics at Scale
Abstract:
Notions of community quality underlie the clustering of networks. While studies surrounding network clustering are increasingly common, a precise understanding of the realtionship between different cluster quality metrics is unknown. In this paper, we examine the relationship between stand-alone cluster quality metrics and information recovery metrics through a rigorous analysis of four widely-used network clustering algorithms -- Louvain, Infomap, label propagation, and smart local moving. We consider the stand-alone quality metrics of modularity, conductance, and coverage, and we consider the information recovery metrics of adjusted Rand score, normalized mutual information, and a variant of normalized mutual information used in previous work. Our study includes both synthetic graphs and empirical data sets of sizes varying from 1,000 to 1,000,000 nodes.
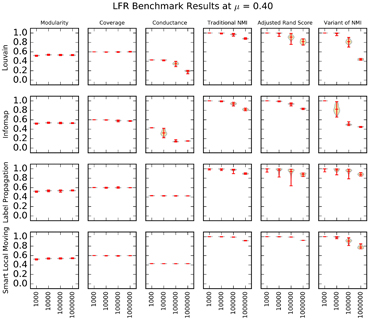
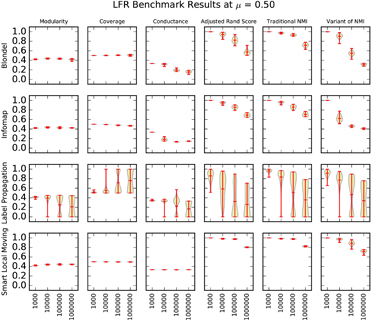
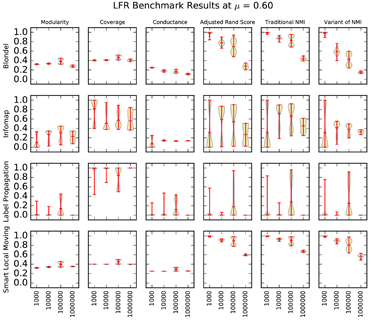
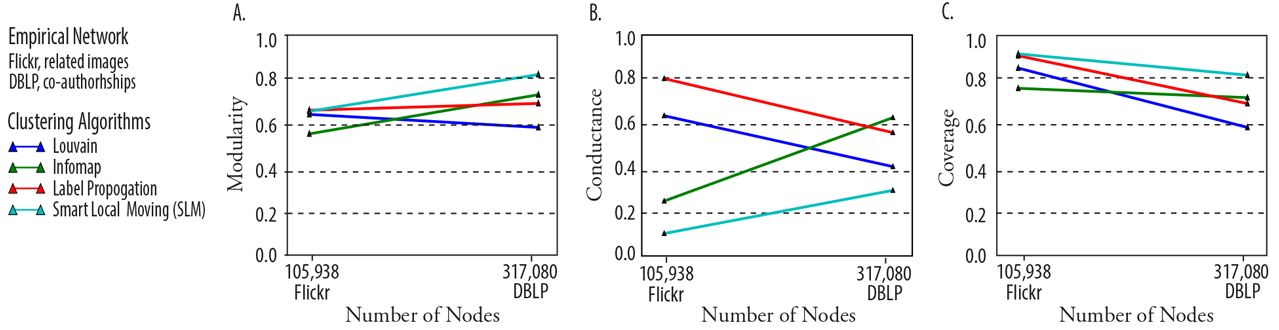
We find significant differences among the results of the different cluster quality metrics. For example, clustering algorithms can return a value of 0.4 out of 1 on modularity but score 0 out of 1 on information recovery. We find conductance, though imperfect, to be the stand-alone quality metric that best indicates performance on the information recovery metrics. Additionally, our study shows that the variant of normalized mutual information used in previous work cannot be assumed to differ only slightly from traditional normalized mutual information.
Smart local moving is the overall best performing algorithm in our study, but discrepancies between cluster evaluation metrics prevent us from declaring it an absolutely superior algorithm. Interestingly, Louvain performed better than Infomap in nearly all the tests in our study, contradicting the results of previous work in which Infomap was superior to Louvain. We find that although label propagation performs poorly when clusters are leusters are less clearly defined, it scales efficiently and accurately to large graphs with well-defined clusters.